Калюжный О.Н.
О рекурсивности психического процесса принятия
решения. Задача о “хорошей” и “плохой” кучках.
Москва, 2005.
В данной статье будет представлена модель, описывающая один из психических процессов, а именно – психический механизм принятия решения.
Эта модель возникла для описания следующего (достаточно известного) эксперимента.
Испытуемому лицу предлагается рассортировать поступающие к нему предметы на 2 кучки: в одну кучку надо положить те предметы, которые ему понравились, а в другую – те, что не понравились. Для чистоты эксперимента лучше, если предметы будут одинаковыми (например, одинаковые шарики), а число поступивших шариков должно быть достаточно велико. Далее вычисляется отношение количества шариков в одной кучке к количеству шариков в другой. Проведение этого эксперимента на практике дает результат, близкий к t = 1,618 … - Золотой Пропорции.
Для объяснения этого результата построим следующую математическую модель.
Пусть в результате рассмотрения очередного поступившего шарика подопытный либо, с вероятностью ½, принимает решение о том, что шарик – “хороший” (т.е. кладет его в кучку A); либо, с вероятностью ½, не принимает такого решения и шарик становится кандидатом на попадание в кучку B. Далее – принимается (с вероятностью p) или не принимается (1-p) решение о попадании в кучку B. В случае непринятия этого решения процесс возвращается на исходную позицию и размышления над этим же шариком начинаются с начала. Вкратце эти размышления можно описать еще и так:
“А хорош ли этот шарик? (Да - A) Если не хорош, то хороша ли моя мысль о том, что шарик не хорош? (Да – B, нет – все сначала, т.е.: “А хорош ли этот шарик?”…)”.
Получился рекуррентный процесс; этот процесс может завершиться как на 1-м шагу, так и на сколь угодно большом, т.е. шарик может рассматриваться бесконечное число раз. Отметим, что вероятность того, что число шагов будет бесконечно, равна нулю.
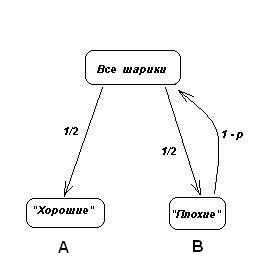
Рис. 1 “Простая” модель
Отметим также, что вероятность попадания шарика в кучку A больше ½, т.к. шарик может попасть в нее не только на 1-м, но и на любом другом шаге.
Асимметрию алгоритма можно объяснить следующим образом. Можно предположить, что размышления над шариком относятся к «сознательному»; в то же время, существует «бессознательное» (априорное) решение, о существовании которого испытуемый не знает. Для утверждения этого решения достаточно одного шага, а вот сомнения могут занять больше времени.
Но это еще не вся схема: необходимо усложнить процесс.
Спрашивается: что это за константа p ? (Будем называть ее вероятностью принятия решения или решительностью) Чем обусловлено ее равенство у всех людей, почему она не зависит, скажем, от возраста или пола?
Для ответа на этот вопрос представим себе, что принятие решения “о
правильности решения о попадании в кучку B” (“решение-
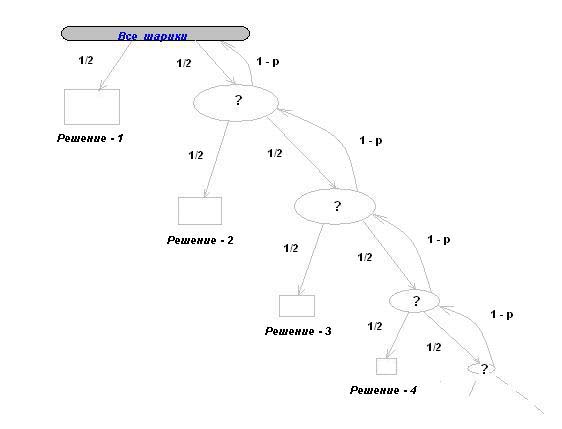
Рис. 2 “Рекурсия вглубь”.
К изучению только что описанной углубленной модели вернемся чуть позже, а пока изучим случай, изображенный на рис.1.
Вычислим вероятность попадания шарика в большую (“позитивную”) кучку A.
P(A)
= 1/2 + (1-p)*1/2*1/2 + (
)2
* 1/2 + …..
Здесь ()k - вероятность того, что шарик
k раз попадал в кучку B, но решение было признано неверным.
Свернем этот ряд и получим:
P(A) = 1/2 *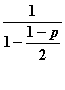 
= 
.
Тогда P(B) = 1 – P(A) = 
и 
= p .
Если перейти от вероятностей к мат. ожиданиям, то, в силу независимости наблюдений:
=
p ,
т.е. искомая пропорция (отношение числа шариков в кучках) и есть вероятность принятия решения, обозначенная как p.
Вернемся к “усложненной” схеме. Хотя в ее описании и отсутствуют какие-либо константы (за исключением 1/2), будем пока манипулировать p – вероятностью принятия решения.
Заметим, что схемы действий на любом из шагов добавленной “рекурсии вглубь” эквивалентны между собой и, следовательно, величина p не зависит от шага. То есть p – “решительность”, независимо от того, в каких условиях она проявляется. На 2-м шаге “рекурсии вглубь”, т.е. при принятии “решения о правильности предыдущего решения” разделим условно кучку B на 2 части: B1 и B2.
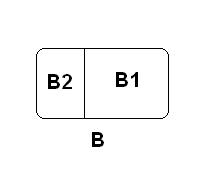
Рис.3
В B1 условно будут попадать шарики, “решение-
Проведя те же рассуждения, какие были проведены для “простой” модели, получим:
P(B2)
= 
, P(B1) = 
.
Таким образом, с одной стороны, вероятность принятия решения о попадании в B
равна p; с другой стороны, она же равна .
Получилось уравнение:
p = (1)
Ранее было показано, что p = 
.
Обозначим пропорцию τ = 
( τ = 1/p ) .
Тогда (1) эквивалентно:
=
,
т.е.
τ 2 / (1+τ ) = 1 ,
т.е.
τ 2 - τ - 1 = 0 .
Единственным положительным решением этого уравнения является Золотая Пропорция!
Получается, что, в рамках описанной схемы, “решительность” любого человека можно обозначить одним и тем же числом, равным Золотой Пропорции.
Отталкиваясь от данной модели, можно построить алгоритм блуждания по графу, порождающий интересный случайный процесс. См. об этом здесь.